La Ley de Números Anómalos de Benford, o por qué la aleatoriedad es más compleja de lo que parece

Revisando una tabla de cifras en la oficina, ante la tentación de rellenarla de manera aleatoria, me vino a la cabeza una curiosidad que leí en algún sitio sobre la detección de fraudes contables mediante una ley matemática completamente contraintuitiva. La anécdota explicaba cómo una de las pruebas del fraude contable de Enron, uno de los grandes escándalos financieros de las últimas décadas, se basaba en que los números de sus estados contables no eran reales porque la distribución de las primeras cifras de estos números no era natural.

El escándalo de Enron fue tan importante que no solo causó su quiebra sino que también se llevó por delante a una de las principales auditoras del mundo, Arthur Andersen, pasando del Big 5 al Big 4 actual. Eso, sin embargo, es otra historia. Hoy centrémonos en las matemáticas.

Frank Benford (1883-1948).

La Ley de Benford, también conocida como Ley de los Números Anómalos o Ley de las Primeras Cifras, dice que en un grupo de números tomados de mediciones o contajes reales, la distribución de las primeras cifras de dichos números no es equitativa sino que los números bajos aparecen con mucha mayor frecuencia. Es decir, que en un grupo de números aparecerá como primera cifra el 1 con una frecuencia mayor que el 5, y el 6 aparecerá más frecuentemente que el 9.

Esto es completamente contraintuitivo, pues la lógica indica que en un grupo de números a priori aleatorios la distribución de las primeras cifras debería ser más o menos del 11,1 % para cada número del 1 al 9. Y esto puede ser así cuando los números son generados "a mano", como en las cuentas ficticias de un fraude contable, pero cuando tratamos con mediciones tomadas en la naturaleza la Ley de Benford se cumple con una precisión asombrosa.

Por ejemplo, tomando las longitudes de los ríos de Europa, el 1 aparece como primera cifra en aproximadamente el 30 % de los números, el 2 en aproximadamente el 18 % de los casos y el 9 en menos del 5 % de los números. Lo mismo sucede con medidas como las superficies de islas del mundo, la  población de países, el número de castañas en cada árbol o la cotización de empresas de un índice. Y lo más curioso es que la distribución se mantiene con independencia de la unidad de medida, ya usemos kilómetros o millas, euros o dólares.

La Ley de Benford no se cumple, sin embargo, cuando hay alguna condición intrínseca a las mediciones o la característica medida no es lo suficientemente heterogénea. Por ejemplo, no aplica en alturas de personas porque casi todas las medidas están entre 1,50 y 2,00 metros. Tampoco aplica en número de habitantes de pueblos, ya que se suele definir pueblo como una población con un número de habitantes entre 500 y 2.200 personas.

En general, la Ley de Benford tiende a cumplirse siempre que los grupos numéricos provengan de mediciones naturales, sean suficientemente amplios y estén libres de condiciones. Se cumple a rajatabla si además las mediciones abarcan varios órdenes de magnitud.

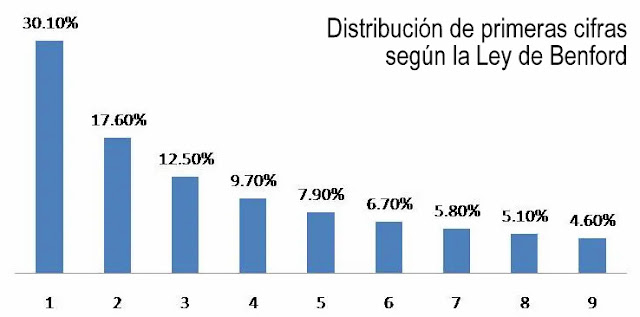
Matemáticamente, la Ley de Benford se representa con la fórmula P(d) = log(1+1/d), donde P es la probabilidad y d es la cifra en cuestión. Calculando, las probabilidades de cada cifra son 30,1 % para el 1; 17,6 % para el 2; 12,5 % para el 3; 9,7 % para el 4; 7,9 % para el 5; 6,7 % para el 6; 5,8% para el 7; 5,1 % para el 8 y 4,6 % para el 9. Esto, además, se cumple para números con cualquier base, no solo con base 10 sino también por ejemplo para números en hexadecimal. Llevando el tema al extremo, podemos calcular que en binario la probabilidad de que un número empiece por 1 es del 100%, como es lógico.

Profundizando un poco más en esta curiosa ley, podemos ver que complicando un poco la fórmula se puede aplicar no solo a la primera cifra sino a cualquiera de las cifras de un grupo de números, aunque cada vez la distribución tiende a ser más equitativa. A partir de la tercera cifra la distribución ya es casi del 10% para cada número entre 0 y 9.

Por tanto, y volviendo al primer párrafo, vemos que la mejor forma de cubrir una tabla de forma aleatoria no es con un generador de números aleatorios tal cual, sino que hay que incluir alguna condición para dar mayor peso a los números que comienzan con cifras bajas. Solo con esta regla se conseguirán números aleatorios realmente naturales.

Lo dicho, la aleatoriedad es más complicada de lo que parece a simple vista.

Puedes profundizar algo más en esta curiosidad viendo la Wikipedia.

COMPARTIR ES BUENO

Tweet

Si te ha gustado este post,
puedes ayudarme a mejorar
con un pequeño gesto :)
→ CLICK AQUÍ ←